Finite State Automata

Introduction

An automata, also known as an abstract machine or model, is anything that is examined in order to find solutions to difficult mathematical problems. The computer science subfield known as the Theory of Automata is intimately connected to the study of discrete systems. In continuation of our discussion of the theoretical aspects of computer science and mathematics, the theory of computation is a subfield that examines the question of whether or not a problem can be solved, and if it can be solved, how well it can be solved if it can be solved at all. This area of study may essentially be broken down into three distinct subfields, which are

1. The Theory of Automata and Other Formal Languages
2. The theory of computational
3. The principle behind computational complexity

Because of this discipline, we have a better understanding of the possibilities and constraints imposed by computers. Another name for the theory that underpins computation is Automata Theory. The term "Automata" can also be used to allude to the concept of "Automation." The Finite Automata is the most fundamental type of automaton. Pattern recognition may be accomplished with the help of finite automata. The finite automata are a type of abstract machine consisting of five parts. It functions according to particular requirements when making the transition from one state to another. In addition, it consists of Accept and Rejects states, which assist the computer in comprehending where the user should get output from the system. The states are determined based on the string of symbols that are supplied. Finite automata can exist in a number of different states; but, at their core, it is only an abstract machine made up of digital machines.
In Finite Automata, there are 5 states that are as follows: {Q, Σ, q0, F, δ }

• Q: Finite set of states
• Σ: A collection of symbols used for input (Automata makes the transition from one state to another based on this input symbol)
• q0: Initial State (Automata starts from Initial State)
• F: A Completed State or Set (Final State is also known as Accepting State. Since there might be more than one final state, we have referred to this topic as the Set of Final State.)
• δ: The Function of Transition

It is important to keep in mind the fact that there are really only two states in finite automata, and they are the Accept State and the Reject State. If the supplied input can be processed without errors and the string can be found in one of its end states, then the input can be accepted. The following is a list of fundamental terminology used in finite automata:

1. Character is another term that may be used to refer to this element. In the Theory of Computation, this component is the most fundamental building element. There is no specific alphabet or letter that must be used.
2. Alphabets can be thought of as either a collection of symbols or a group of characters. Alphabets are always considered to be part of a finite collection.
3. A string is defined as an unbroken succession of the same kind of symbol. It is made up of glyphs, which are also known as characters.
4. The occurrence of a particular character one or more times is referred to as positive closure. Positive closure occurs when a character appears more than once. This indicates that null Strings are not permitted to be used. The notation L+ is used to indicate it.

Kleene Closure indicates that a specific character has appeared zero or more times. It only suggests that null Strings can also be tolerated in some circumstances. It is denoted by the letter L. It is possible for a language to have a total string count of 2n, where n is the length of the longest string in the set being considered. Another way to write the Kleene Closure is as L = L+ + ε, where ε is a null character or an identity element. This is another way to describe the Kleene Closure.

Grammar is a finite set of rules that, when followed, result in syntactically accurate sentences. In the theory of computing, grammar is referred to as "the language of computation." The four tuples—noun, pronoun, verb, and object—comprise the formal definition of grammar. G = (V, T, P, S)

1. It is possible to produce the strings of a given language by utilizing something called grammar, which is denoted by the letter G and contains a set of production rules.
2. Lowercase letters represent the last set of terminal symbols, which are symbolized by the letter T.
3. The final group of non-terminal symbols is made up of capital letters, which represent the letter V.
4. P is a collection of production rules that may be applied to a string in order to replace non-terminal symbols in the string with other terminals.
5. The string may be derived by beginning with the letter S, which is the start symbol.

There are three distinct categories that may be used for finite automata:

Deterministic Finite Automata:

The machine in deterministic finite automata, also known as DFA, only ever enters the state that corresponds to the particular input character that was given to it. Each input symbol possesses a transition function that is predefined for each and every state. In DFA, null is strictly forbidden, and the state of the variable cannot change if the input character is left blank. The first and most important step is to identify a pattern from which numerous DFA may be developed. However, the DFA that has the fewest number of states is considered to be the superior DFA. Let's have a look at a working example of DFA that recognizes all the strings beginning with 0. Diagram of the Transition:

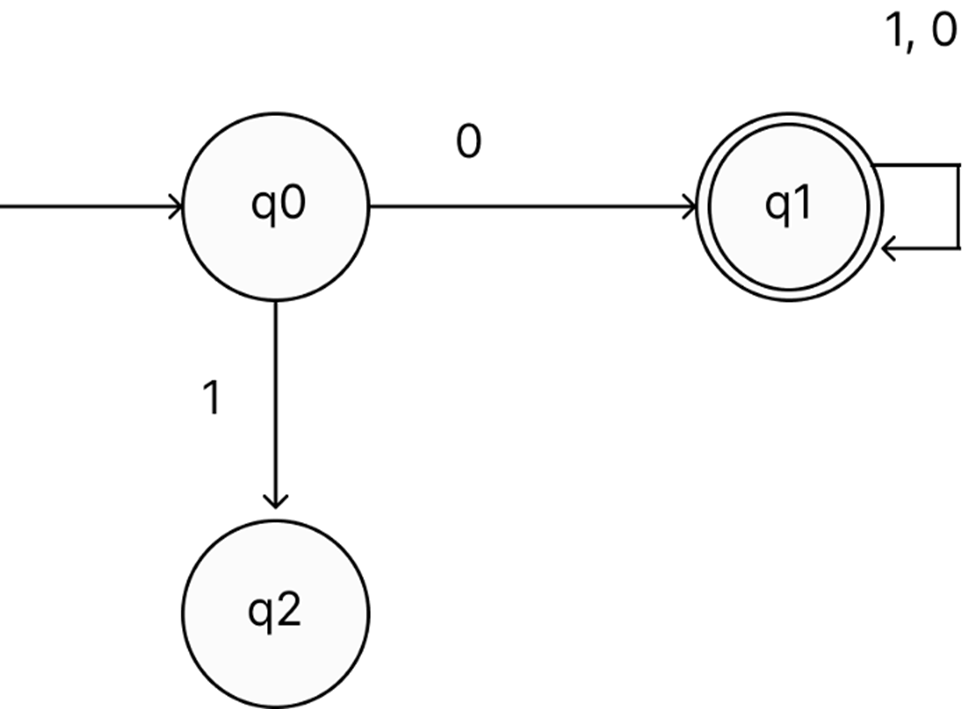
The DFA, which is represented by the transition diagram shown above, is the one that recognizes strings that begin with 0. The operation of this Finite Automata takes place as, first, the first state (q0) receives the input 0 and then makes the transition to the final state (q1) following the transition. If, however, the first character that is input is a 1, then q0 will make a transition to q2 which is the dead state, or we can call it a reject state because it indicates that the current string has been rejected by the Finite Automata. Additionally, on the final state, we will make transitions to ourselves whenever we receive the input of either 0 or 1 which will indicate that the string can end with either 0 or 1. On the basis of the construction and operation of DFA, we are able to assert that the language is made up of input strings such as 0, 00, 01, 001, 010, etc.

Various DFA Applications • DFA is put to use for a wide number of purposes, including voice recognition, protocol analysis, text parsing, analyzing character behavior in video games, performing analysis of computer security, and controlling CPU control units.

• DFA is utilized in vending machine settings.

• The lexical analysis performed by the compiler has made use of it.

• Utilized in regular expressions so that the pattern may be recognized.

Non-Deterministic Finite Automata:

For each particular piece of input in a Non-Deterministic Finite Automata (NFA), there is the possibility of a transition to one or more states. This indicates that the automata may be in more than one state at any given time, depending on the symbol that was used as input. Because of this, we refer to it as a non-deterministic process. It does not allow any movements that are null. Let us look at an example of NFA, which is able to process strings beginning with any number.

Diagram of the Transition:

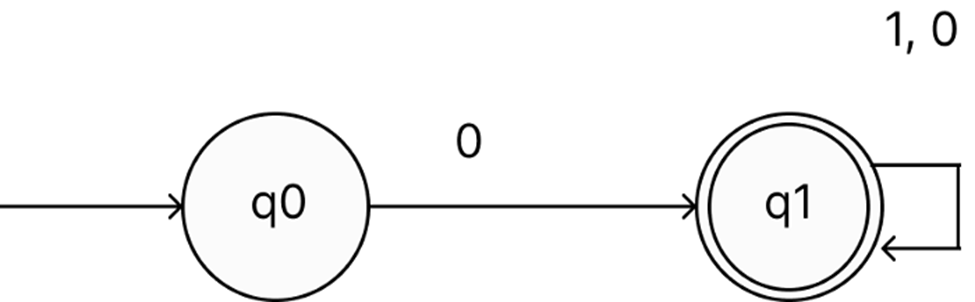
The NFA, which recognizes all the strings beginning with 0, is depicted in the transition diagram that you can see above. The operation of this finite automaton is really simple, as we can see from the fact that, initially, the first state (q0) receives the input 0, and then it proceeds to transition to the final state (q1) after reaching that point. Because there is just a transition of 0, we are able to declare that Dead Configuration has happened and the string will be rejected if we get the input symbol as 1 from q0. This is because there is only a transition of 0. In addition, in the final state, when we receive the input 0 or 1, which indicates that the string might finish with either 0 or 1, we make transitions to itself, which means that we are returning to the initial state. In light of the structure and operation of NFA, it is possible for us to assert that the language is made up of input strings such as 0, 00, 01, 001, 010, etc.

Epsilon-NFA (ε-NFA): In the context of non-deterministic finite automata with epsilon movements (ε), it is possible for an automaton to be in more than one state given the same input symbol. Epsilon motions are permitted to be made in this particular automaton. That is to say, automata are able to function without needing to read symbols. It has the capability of transmitting to any number of states in response to a specific input. Crucial points:

1. Every NFA and -NFA is also a DFA, but vice versa is not the case.
2. Every -NFA is also an NFA, although the converse is not necessarily true.
3. The DFA does not let many options to correspond to a single input, but the NFA does permit this.
4. Compilers make considerable use of DFA at the Lexical Analyzing step of the process. We can disassemble strings into tokens with the assistance of Lexical Analyzer.
5. In NFA, the concept of "Dead Configuration" refers to the possibility of excluding a given string from the Automata in the event that no transition has been specified for a certain symbol. Whereas in DFA we are required to demonstrate the transformation of such symbols into their Dead State equivalents.
6. When compared to NFA, DFA is far more challenging to both create and comprehend.
7. NFA is more of a conceptual idea at this point.

Applications of NFA

• NFAs were used to simplify the mathematical effort required to show a number of fundamental facts in the theory of computing. This reduced the amount of time spent on the proofs.
• When it comes to demonstrating the closure properties of regular languages, NFAs are a significant step ahead of DFAs in terms of their utility.

Mealy and Moore Machine

Mealy and Moore machines finite state machines that give output

Moore Machine

Moore’s machine is essentially an example of a finite state machine, in which the subsequent state is determined by the present state. The only thing that determines the output symbol is the current state of the machine. The Moore Machine may be described as having the notation (Q, q0, ∑, O, δ, λ) where,

1. Q: a finite set of states
2. q0: the initial state
3. ∑: a finite set of input symbols
4. O: output alphabet
5. δ: transition function where Q × ∑ → Q
6. λ: output function where Q → O

An example that is simple to comprehend for the Moore Machine,

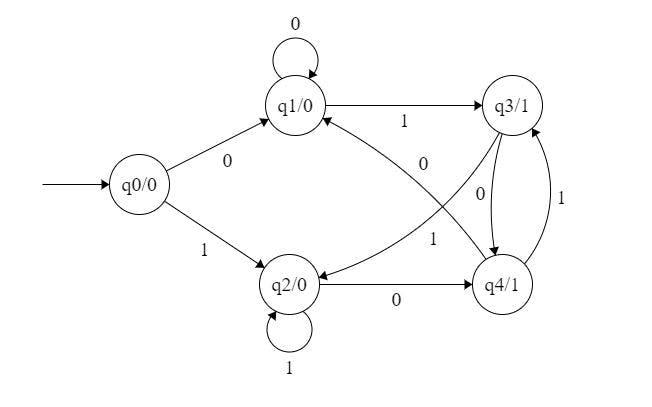
In the example that follows, the Finite Machine is constructed in order to verify the parity of a given number; specifically, if we obtain an odd number of ones, the output will be one, but if we get an even number of ones, the output will be zero. You can see this in action in the following diagram. In accordance with the manner in which the Moore Machine operates, the transition diagram is made up of the states that are related to the output.

Moore Machine's Many Uses and Applications

1. Moore State machine is used as a right enable in SRAM due to its fast speed, which makes it an ideal candidate for this role.
2. Moore machines are essential tools for the construction of combinational as well as sequential circuits.
3. Imagine an elevator, in which each condition would represent a new floor. You are able to modify the status of the system without providing any more input if you only hit a button to advance to a specified floor.

Mealy Machine

A Mealy Machine is a type of machine in which the output symbol is dependent not only on the current input symbol but also on the state in which the machine is currently operating. In this case, the output is represented by the combination of each input sign and the slash character (/). The Mealy Machine is described as having the following components: (Q, q0, ∑, O, δ, λ) where

1. Q: a finite set of states
2. q0: the initial state of the machine
3. ∑: a finite set of the input alphabet
4. O: output alphabet
5. δ: transition function where Q × ∑ → Q
6. λ’: output function where Q × ∑ →O

An example that is simple to comprehend for the Moore Machine,

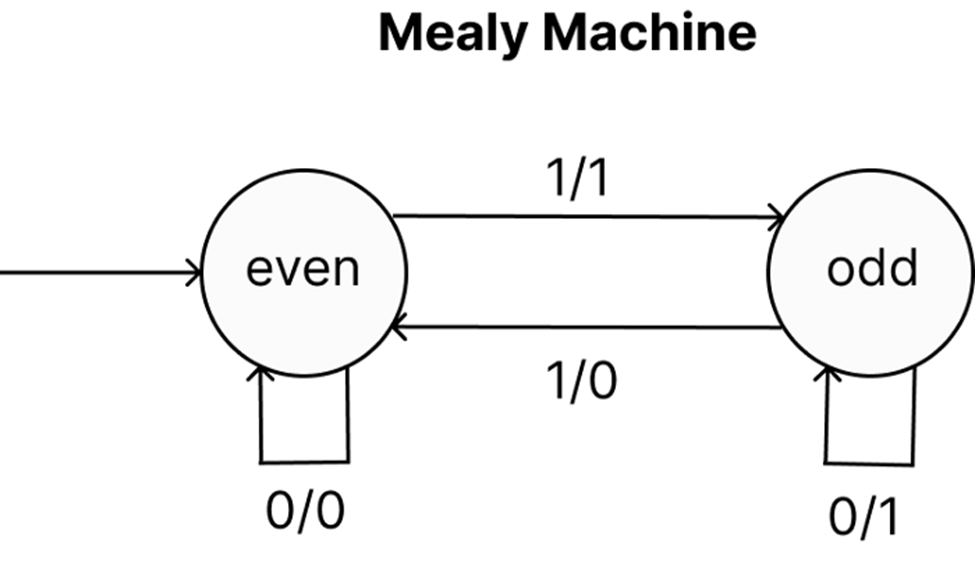
In the example that follows, the Finite Machine is constructed in order to verify the parity of a given number; specifically, if we obtain an odd number of ones, the output will be one, but if we get an even number of ones, the output will be zero. You can see this in action in the following diagram. In accordance with the manner in which the Mealy Machine operates, the transition diagram is made up of the transition arrows that are related to the output and is organized as follows: input/output.

Examples of Uses for the Mealy Machine

1. As a result of its ability to have numerous states, Mealy machines are employed in processors.
2. Mealy machines have contributed to the development of cipher machines by providing a fundamental mathematical paradigm, which is useful for these devices. We are able to design a mealy machine for any given string of letters by taking into consideration the Latin alphabet both as the input and the output. This allows us to turn the provided string of letters into a string that is encrypted.

---

Thank you! If you have any doubts, feel free to ask them in the comment section.